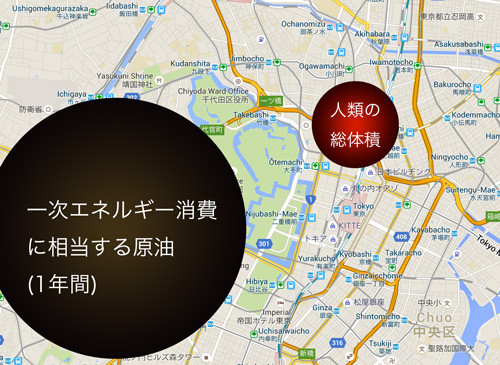
人類は直径1kmの球体容器に詰めることができる
人類の質量はどのくらいだろう。
仮に70億人x70kgで見積もったとして4.9億トン
人類の平均体重を70kgで見積もっても大きく超過することは無いだろう。人類の歴史を紐解くと700kgを超えるような個体もあるが例外的だ。世界を見渡してみると質量の小さな未成年が結構な割合をしめているし,肥満に悩まされているのは一部の先進国だ。おそらく真の平均は70kgより低い。
直径1kmの球形容器を水で満たすと約5.2億トンであり,肺の空気を抜くと人間の比重は1を超えることから,挽肉か何かにして隙間を完全に無くせば,恐らく地上にいるすべての人類は直径1kmの真球に納まるだろう。
直径1kmに納まる有機体を支えるために必要なもの
人類が2013年に消費した一次エネルギーは石油換算で127億トンで,直径3kmの球体に相当する。*1
水の年間消費量は,4兆トンくらいで直径20kmの球体に相当する。人類は農業や工業をはじめとした様々な用途で,毎時毎時自分の体重と同じくらいの水を消費している。
人類のエネルギー起源の二酸化炭素排出量は,環境省によると年間317億トンで*2,標準状態を仮定すると直径31kmの球体に相当する。ただし,気体は密度(または比容)が圧力に強く依存するため,実際に直径31kmの球体に二酸化炭素を詰めると,上と下で何倍もの密度差が生じる。
人類が呼吸で1年に消費する酸素は15億トンくらいで*3,大気は1km^2あたり210万トンの酸素を含むので,1年で東京23区あるいは琵琶湖の上空にあるすべての酸素を消費しつくす程度。無論,化石燃料の燃焼によって消費される酸素に比べれば少ないし,地球全体の酸素にくらべれば微々たるもの。
球体による可視化
日常的でない量を伝える文章では,様々な「原器」が用いられることがしばしばある。例えば,高さや体積を東京タワーや琵琶湖,富士山などで表現する手法だ。今回は,そのような原器を使うこと無く,単なる球体を使った表現で,大雑把な量的感覚が伝わるか試してみた。人類という存在が物質的にどのくらいの規模で,それを支えるのにどのくらいのリソースを必要としているか,すこしでも感覚が伝わると嬉しい。
*1:資源エネルギー庁 http://www.enecho.meti.go.jp/about/whitepaper/2015html/2-2-1.html
*2:環境省:2012年の二酸化炭素排出量 http://www.env.go.jp/earth/ondanka/shiryo.html
*3:国際宇宙ステーションの酸素消費量0.84kg/dayを採用すると21億トンくらいになりそう
君の部屋にリモコンはいらない
午前5時,真っ暗な部屋の中で目が覚める。
記憶を頼りに,もぞもぞと部屋を明るくするリモコンを探してボタンを押す。
そういうのは21世紀の生活ではないだろう。もう映画『Back to the Future』でデロリアンがたどり着いた時代だ。未来的でなくともいいが,もっと時代にふさわしい生活がある。いちいちヒトが機械にリモコンで指示を出すのは00年代までで十分だ。
大量のリモコンをどうするか
恐らく,一般的な家庭には,エアコン,テレビ,室内灯,空気清浄機といった様々な家電に対応したリモコンが存在する。そうしたリモコンをたくさん並べて操作するのは現代的ではないが,これを解決する手段として挙げられる学習リモコンもまだ理想には遠い。学習リモコンを携帯している人は少ないし,UIが使いにくいものも多い。
スマートフォンを万能リモコンとして使うツール類はある。携帯していることが多いので学習リモコンよりややマシだが,家では充電器に繋がれていることも多く,ワイヤレスなデバイスではない。
「考えただけで動く」の先にある家電
いつの日にか,家電は脳インプラントもなしに「考えただけで動く」ようになるのかもしれない。ただ,そこは人類の目的地ではないだろう。「考えないでも動く」ものであって欲しい。
高度な断熱材に囲まれ全館暖房と温度管理が行き届いた部屋において,人間は毎日のように室温のことを考え,機械を操作したりする必要がない。
ロボット掃除機がある部屋において,人間は,いつ掃除をしようだとか,どこから掃除をしようだとか,そんなことに意識を使うことはない。
廊下やトイレに行くとき,明かりを付けるだとか消したりといった動作を考える事はない。勝手について勝手に消えるからだ。
リビングの明るさは外光を補正して自動調光され,冬場の遅い日の出を待つこと無く起床予定時刻に合わせてゆっくりと明るくなる。
そして人間が考えないでも動くだけでなく,機械が生活の事を考え,人間を調律し教育さえするものであって欲しい。現に,いまこの文章を書いている部屋は,Roombaによって,床に一切のものを放置してはならないという圧が作り出されている。
人間が存在を忘れるような存在へ
ルーチン的なちょっとした意識配分,集中作業を分断するちょっとした手間,その種のコストを削ることには,それなりの金銭を払う価値がある。そして,それは1億2億ではなく,普通の市販品で十分実現できる領域にある。
機械の気遣いと人間の快適さが衝突する場合はいくらでも残るだろうから,しばらくは,仕方なく,会話などで修正することになるだろうが,可能な限りの自動化を望んでいる。
人為的な操作が限りなく遮蔽され,認証された音声でしか操作できない状況になれば,権限のない者が不用意に電化製品を操作することも減っていくだろう。例えば,猫や赤子が誤ってリモコンやストーブのボタンを押してしまうといったようなことは,過去のものになる。
そして,いつの日にか,リモコンが何だったのか忘れるような時代になってほしい。*1
大雨の激しさは何が限界を決めている?
広島で,10分間に20mm以上,1時間に130mm,あるいは2時間で200mmに達するような猛烈な雨が降り, 多数の土砂災害が発生した。
ただ,世界を見渡すと,1分間で38mm降っただとか(2280mm/h),8分で126mm降っただとか(945mm/h),瞬間的とはいえその10倍を超えるような想像を絶する短時間強雨の記録がある。降水強度は100mm/hあたりに物理的な限界があるわけではないようだ。
世界記録を確認するため米国海洋大気庁(NOAA)のサイトを覗いてみよう。
http://www.nws.noaa.gov/oh/hdsc/record_precip/record_precip_world.html
World record point precipitation measurements
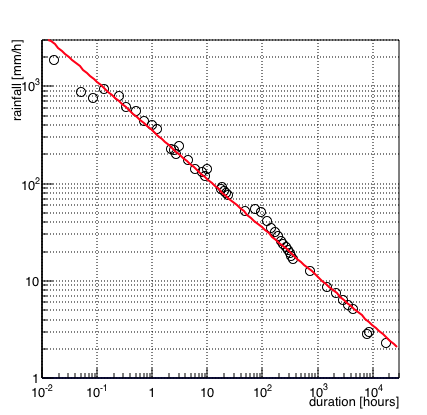
時間が短いほど降水強度の記録が大きいことは当然に予想されたことだが*1,値を図1のようにプロットしてみると,大雑把に時間の -0.5乗に比例することに気づいた。しかも,恣意的に選んだごく狭いレンジではなく,上記リンクの全データ,1分から2年間にいたるまで幅広く成立する。
図1: 降水強度Rと継続時間Tの関係
横軸が時間(h)で縦軸が降水強度(mm/h)
○は実データであり,赤線は R=350/sqrt(T)
放射性壊変のように完全に独立な事象ならともかく,ある時刻の降水量と別の時刻の降水量が密接に繋がり,周期性や季節変化などもある現象で,単一の冪でこれだけ表現できるのは意外であった。
地球の平均降水量は0.1mm/h (~1000mm/y) ぐらいであり,雨の多いところで大雑把に1mm/h (10,000mm/y)なので,時間を大きくしていく極限では1mm/hくらいに収束するだろう*2。一方で,短時間の極限でどこまで降水強度が上がるのかはグラフや記録からは読み取れない。個々の雨粒を分解するような短い時間になると,適切な降水強度の定義を考える必要がありそうだ。
私は短時間強雨の世界記録がどういう物理によって制約されているのか不勉強で計算できる水準にない。(10m/s)*(10g/m^3) = 360mm/hなので,大雑把には空中に保持できる雨粒の限界と,地面に叩きつける速度,湿った温かい空気の供給速度などが,限界を決めているのだろうと想像しているが,細かなプロセスまで含めて基礎的な過程から導出したい。
そんなにすぐに答えが分かるとは期待していないが
検索すると,下のように個々の記録について評価したものや,あるいは図1と同じ内容のグラフはいくらか見つけた。
https://www.jstage.jst.go.jp/article/jjshwr/23/3/23_3_231/_pdf
(どういう物理でそうなっているのか知らないが)降水量は,対数正規分布に従うだとか,ガンマ分布に従うといった文献も見つけた。
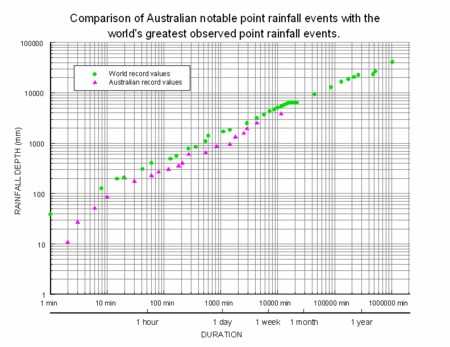
気候によって冪が違うかも知れないし,オーストラリアの極値を見る限りでは,短時間極限で降水強度の頭打ちがあるようにも見える。
http://www.bom.gov.au/water/designRainfalls/rainfallEvents/worldRecRainfall.shtml
ちゃんとやるには片手間では済まず作業量が発散しそうなので,今日はこの辺で。
(詳しい方の解説は大歓迎です。)
新たなる道
新生活のバタバタで遅くなってしまったが,4月から新しい場所で新しいことをしていることを報告しておきたい。
どこからどこに遷移したかはこの場ではお答えすることができないが,大学から別の公的セクターに移っただけであるし,身分を含めて様々な変化があったとはいえ,やることの基本はあまり変わった気がしない。コミュニケーションが大事であること,装置や物理現象・数式に関する十分な理解を必要とすること,共通点は他にも無数にある。
ここまでくるのに色々なことがあった。厳しかった方,根気よく指導してくださった方,悩みなどを相談した方,様々な手続きをしてくださった方,食堂などで日々会話をした方,そうした非常に多くの素晴らしい方々のお陰で今この場所にいる。そのことについて心から感謝したい。
本当に,ありがとうございました。
そして,これから5年10年,よい結果がだせるよう精進していきたい。
万里の長城の内側から
はてダは見れるようなのでテスト投稿
まだ何がつながって何がつながらないのかよくわからないな。ヒウィヒヒーがみれないのは予想された通りだけど、はてブも見れないし。
この程度のことを書いても「こんな夜中に誰だろう」にはならないとは思うが恐る恐るポスト
人工知能:東大入試からシンギュラリティまで
メディアや他の方がいくつか報告を上げているが、土曜日に『ロボットは東大に入れるか』の講演を聞きに行ったので気づいたことなどをメモしておこう。
人工知能にとっては、センター数学よりも東大二次数学の方が解きやすいことや、図形や文の構造を理解することがどうしようもなく難しいことなど、AIと人間の違いに関するいくつかの側面を興味深く受け取った。
「人間のように思考する」といった曖昧で高すぎる目標ではなく到達度を客観的に評価しやすい入試問題をターゲットに選んだのはよい着眼点だと思う。もし2021年までに、東大入試クラスの読解力や問題処理能力を獲得したならば、技術文書を要約したり、国会答弁を自動生成したり、様々な産業応用が可能になるだろう。
模試の結果はもっと惨憺たる有り様になると思っていたが、センター試験では 387/900、2次試験は(今回は数学のみだが)合格者平均を超えるなど、予想していたより結構できていて感心した。まだまだ合格までの道のりは長いとはいえ、現代文ですらそれなりに点をもぎ取っているのが面白い。
数学
数学は特に興味を引かれた。解けてる。
コンピュータによって自動的に定理を証明する試みは古くから行われてきたが、数学の研究は未だに自動化出来ていない。しかし、いつの日にか人間を遥かに超え、想像もつかないような数学の世界を示してくれることを期待している。
今回の数学は以下のように求めている。
- 問題文を言語解析し、論理式(一階述語論理)に変換する
- 論理式を書き換えて、数式処理システムが扱える形式に変換
- 数式処理システムが、解答を作成し出力。
ほとんどの数学は一階述語論理とよばれる論理式で表現することができる。日本語で書かれた問題を、論理式に変換するのが第一ステップだ。ここだけはまだ半自動で、人の手が介在する。論理式に正確に置き換えることができれば、あとは完全自動でMathematicaのような数式処理システムが限量記号消去法(QE)などを用いてゴリゴリと等価な式に変形し、解答を作成する。
例えば、『すべてのxに対して
が正となるようなa,bの条件を求めよ』という日本語の文章を『
』という論理式に置きかえて、これをQEによって等価な式に書き換えながら
のような限量記号を消去し、『
』という答えを見つけ出す。
問題文を論理式に変換できたからといって必ず解ける訳ではない。定式化のやり方によっては、コンピュータで解けないほどの計算量になる場合もあるし、まだ実装が不十分でちゃんと扱えない単元もあるようだ。現在の東大入試ロボットは、微積や数列、代数・幾何などは比較的得意でも、三角関数や整数論が苦手だったりまだまだ改善する部分はある。
特徴的な答案
解答は人間の答案とは似ても似つかないが、絶対に計算ミスしないし、正解した時は完全に正しい答案になるのでその大問は満点だ。外れれば0点である。『人工知能』という名のホームランバッターに部分点はない。解答はどんな分野の問題でもすべて同じフォーマットになる。
問題文は次の論理式と等値である。〜論理式〜 この式は実閉体の体系RCFの式であることから、ほげほげの定理により、このしきと等値で量化子を含まないような式を求めることができる。ほげほげの量化子除去アルゴリズムをつかって、上記の式を書き換えた結果が以下の式である。 答えがズドン
文系理系ともに、2大問をこのような解答で満点を取り、1大問は計算量が爆発して解答に辿り着けず、残りは白紙という結果。これでも偏差値60になるが、当たり外れが運次第なので成績は安定しない。
人工知能にとってはセンター数学のほうが難しい
数学ロボットが面白いのは、人間と違って2次試験の方が得意なことだろう。問題文が論理的で簡潔であればあるほど解きやすくなる。人間にとっては東大生の2%しか完答できないような難問であろうとも、問題文が明確でありさえすればあっさり解けたりする。
逆に、センター試験のように問題文が長くなり誘導を付けられると人工知能は苦戦する。途中でちょっと転ぶと後は全滅だし、多数の文の関係を評価する国語力が求められる。そもそもロボットと人間では思考の流れが全く異なるので、人間の思考に沿った誘導は親切どころか撹乱にしかならない。
しかし、結果はなかなかのものだ。例えば数IAなら、全部で4設問あるうちの最初の2つ(方程式・論理・二次関数)は満点を取るなど、上手くフィットすればしっかり解ける。残念ながら第三設問(三角比・平面図形)の途中で躓いたあとはすべて白紙だが、57点を獲得し平均点を超えている。
ちなみに第四設問は『場合の数と確率』で、これはコンピュータにとって相当な国語力が要求されるのか0点である。「カードを取り出してシャフルした後、印をつけ」みたいな多様な文を論理式に変換するプログラムは大変らしい。
国語
次に興味をもったのが国語だ。文章を適切に解釈することはすべての科目に通じる重要な課題だ。「読解力とは何か」という問いにはまだ手がでないので、とりあえずは「点数が解ければよかろうなのだ」の方針で試みているそうだ。
文章を理解していなくとも、単語ベースの手法で傍線部解釈問題をそれなりに選べる事には驚いた。しかし、ダミー選択肢を作る手法としてよく用いられる論理の逆転には瞬殺される。
今回のセンター模試は、小論18点、小説24点、古文20点と振るわなかったようだが、ランダムに選ぶより有意に高い。小説は絶望的かと思いきや結構取った。現代文では、68点をとったこともあるそうだ。
予想よりできているのは喜ばしい。だが、文の構造を理解できるようにならない限りさらなる高みは難しいだろう。センターは適当にお茶を濁せるかもしれないが、2次試験はワードサラダみたいな答案では通用しない。
すこし外れるしうろ覚えだが、『傍線部が指し示すもの』が傍線部のどこに分布しているかみたいな統計データは興味深かった。上のグラフは実際のデータではないが、傍線部の前後にピークを作る。その分布に合わせて重率を掛けて単語をマッチングしていったりすると面白い。
英語
英語の結果が悪いことには驚いた。センター英語は正答率が26%なので、ランダムに選んだのとさほど変わらない。すべての科目の中で一番悪い。解けていると言えるのは、発音・アクセント問題だけだ。
英語が125点くらいまで上がれば全科目の合計が受験生の平均点を超えるし、伸びしろは沢山あるので今後の進展に期待したい。
ただ、東大生のセンター英語の正答率は96%だそうなので、その水準に達するには凄まじい改善が必要だろう。そのレベルに達したならば、Google Translateをはるかに超えるAIが出来ているはずで、逆に言えばGoogle並に何百億と研究費を投じても簡単ではないだろう。
物理
物理シミュレータに放り込んで数値実験という発想は無かった。数学よりも国語力を必要とし、図形解釈もあるので先は長い。文章から状況を復元するのは人工知能にとって非常に難しい問題だ。そして物理の問題には書かれていない常識がたくさんある。
例えば、これは途中で宙返りするジェットコースターの図だが(東大2010)、これが『曲線と円が接している』ではなく、この線がひとつながりの線路であることを認識しなければならない。問題文と図を使った複合的な理解が求められる。
社会(日本史&世界史)
歴史がそれなりに取れるのは予想していたので特に驚きはない。両方共6割弱といったところで、他の教科と比べて悪くはない。ただ、東大を目指すなら9割はほしいので、深い文章理解という壁がまた立ちふさがる。
総評&その他
2次試験でどのくらい悲惨な答案をつくるか期待していたのだが、今回は数学以外はトライしていなようで残念だ。
文章の理解に関しては、まだ目標の1%にも達していない印象を受けたが、人工知能ワトソンも最近まではさんざんだったのでブレイクスルーがあるかもしれない。そして、文章を理解できなくとも、多くの私立大学に合格する成績を叩き出せることは新鮮だった。
人工知能研究はなかなか思うように進まずブームと冬の時代があり、エキスパートマシンや第五世代コンピュータといったある意味では黒歴史のような単語を聞けたのはよかった。最近は、GoogleやAppleなどが人工知能研究に膨大な投資を行っており、第三の波が訪れつるあるそうだ。Googleは様々な人工知能を研究しており、例えば自動運転は既に50万キロ走り人間より事故率が低い状況にあるそうで、担当者が「人間は運転に向いていない」と豪語するまでになっているという話など、AIについて明るい展望も聞いた。
未来:人工知能に期待すること
ある決まったフレームの元であっても、問題を理解しそれに対して適切な答えを作ることができる人工知能が生まれたら、それは驚くべき進展だ。そして、それは東大入試ロボットが目指す2021年では恐らく無理だろう。しかし、実現を願って止まない。
クイズ王を下した人工知能ワトソンが医療データの検索支援やヘルプディスク・コールセンターに応用されつつあるように、そのような人工知能は人間がやらなければならない仕事を減らしてくれることだろう。
特に、専門知識が必要で頭を使う必要はあるがクリエイティブでない仕事は、将来、人工知能で一掃しうるだろうし、そうなることを期待する。
そして、クリエイティブさを定義するのは厄介だが、最終的には創造的な仕事を含めたあらゆる仕事を代替できるようになってほしい。既に、人間の脳という機械が宇宙に存在している以上、原理的にはそれを同等の機械をつくることは物理学的に禁止されておらず、おそらくそれを越えたパラメタの機械を作ることも可能だろうし、いつかできてほしい。
人間が有利な領域がどんどん狭くなっていく過程で、「知的」の定義も人間に都合よく書き換えられていくだろうが、最後に残るものを見届けたい。
その時代に旧人類が何をして生きていくかは経済学者なり社会学者に任せるとして、ポスト・ヒューマンないしシンギュラリティが地上に現れる様を私はみたい。人間の領域をはるかに超えた科学、すべての自然科学者を失業させるほどの知の体系を見ることができるのであれば、経済的にいかに不利益を被ろうとも構わない。