宇宙の果てや加速膨張はどう観測されるか
宇宙をのぞきこんだとき、最も深い世界はどう見えるだろうか。
ちょうど2011年のノーベル物理学賞が『宇宙の加速膨張』になったので、現在観測される宇宙の全体像について簡単に触れてみよう。例えば次のような誤解を聞くが、実際はどうなのだろう。
誤解の例
- 同じ大きさの物体は遠くにあるほど小さく見える。
- 100億光年はなれた銀河は、100億年前に100億光年離れた場所にあった。
- 宇宙は光速で膨張している。
- 宇宙が2倍になると原子の大きさも2倍になる。
A. 超遠方宇宙の概要
宇宙といえど無限の奈落ではない。夜空を見上げた視線は観測可能な宇宙の果てにつきあたる。超遠方の天体は宇宙の果てに近いほど次の性質を示す。
- 若い
- 赤い
- 時の流れが遅い
- 大きく見える
- 暗い
A1. 遠い宇宙は若い
遠い宇宙は太古の宇宙だ。遠い宇宙から地球に光が届くのには時間がかかる。遠くを見ることは、過去を見ることであり、遠くの宇宙は近くの宇宙より若々しい。例えば、数十億光年先の世界は星の出生率が概して高いし、高齢者の割合は少ない。
Fig1. 我々が観測する宇宙の全体像
目盛は宇宙年齢を示していて単位は10億歳。左端の望遠鏡が地球の位置で137億歳を指している。
遠くを見れば見るほど宇宙が若かった時代を見ることになり、どの方向を見ても行き着く先にはビックバンがある。然るべき観測装置があれば、宇宙の再電離が完了した時代、最初の銀河が生まれた時代、最初の星が生まれた時代、まだ星すら存在しない暗黒時代、そしてビッグバン直後の宇宙が光に満ち溢れた時代*1に到達する。ちなみに、満ち溢れていた光はまだ宇宙をさまよっているが、赤方偏移(後述)でマイクロ波まで引き伸ばされているので肉眼で空を眺めても真っ暗闇だ。
光が届くのに1年かかる距離を1光年(LTD: look back time distance)と呼ぶことにしよう。ビッグバンまで約137億光年(LTD)離れており、人類が所持する望遠鏡の射程距離は130億光年(LTD)*2を越える世界に到達しつつある*3。
A2. 赤方偏移:すべては赤くなる
宇宙が本当に膨張しているかはさておき、遠くの天体は赤い。遠ければ遠いほど赤くなり、ニュースに出てくる最遠部の銀河ともなると赤外で光ってる。(赤外望遠鏡は大事)
物体からくる光が本来より赤くシフトする現象を「赤方偏移」という。固有運動*4や天体の収縮や重力なども寄与するが、遠方天体の大きな赤方偏移はほとんど宇宙膨張によって説明される。
宇宙膨張による赤方偏移の量を、後退速度という概念を経由して説明するのは、高赤方偏移天体クラスの距離になると厄介なので、素直に「宇宙がX倍に膨張すると、光の波長もX倍に引き伸ばされる」という一般相対性理論のシンプルな関係に頼ることにしよう。
Fig2. 赤方偏移と距離(LTD)の関係
赤方偏移で波長がX倍に引き伸ばされる時、赤方偏移の指標ZをZ=X-1で与えよう。例えば、15%引き伸ばされる(X=1.15)ならZ=0.15となる。天の川銀河近傍がZ=0で、Zが大きいほど遠方の天体であり、Z=1が宇宙が今の半分だった時代に対応する。宇宙の果てで無限大に発散する。
また、Zが1より十分に小さいところでは以下の関係が成立する。
天体までの距離〜 Z * 135億光年
天体の後退速度〜 Z * 光速
(例えば、Z=0.04 だと、5.4億光年離れていて光速の4%で遠ざかっているように見える。)
A3. 遠い宇宙ほどスローモーション
近い銀河はほとんど1倍速だけど、遠い銀河になるほどゆっくり時間が流れているように見える。光がX倍に伸ばされるとは光の周波数が1/X倍になることであり、さらに言えば、光の周波数だけでなくあらゆる変動が1/X倍速になって観測される。
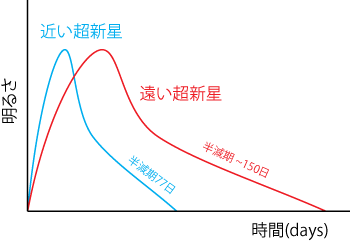
Fig3. スローモーションの実例:Ia型超新星の明るさの変化
Ia型超新星の明るさの変化は、生成された放射性物質の半減期で決まっている。本来、コバルト56の半減期は77日だが、遠い超新星はコバルト56の半減期が伸びて(例えば150日)観測される。
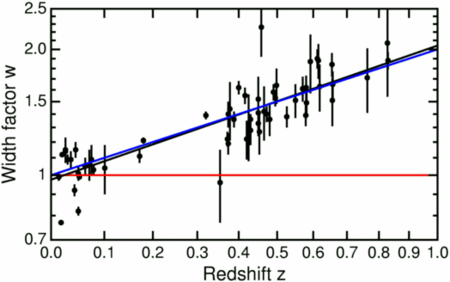
Fig4. 距離とスローモーション効果の実測
(横軸)赤方偏移Zに対して、(縦軸)超新星の光度変化が何倍スローモーションになって見えたか(light curve fitting)
時間の流れが1/(1+Z)倍 (1/X倍) になっていることが確認できる。
最遠の世界は単に若い頃の宇宙であるだけでなく、時が凍りついたように年を取らない。
A4. あまりに遠い天体は逆に大きく見える
「物体は遠くなるほど小さくみえる」これは我々の日常空間では常識だ。太陽系や銀河団といったミクロな世界でもそうだろう。
しかし、宇宙の底に届くような距離では違う。
まだ宇宙が小さかった頃に天体を出発した光がつくる像は宇宙膨張によって果てしなく引きのばされてしまう。この宇宙では約100億年光年(LTD)離れた物体が一番小さく見える。これより長い距離では膨張の効果が勝ち、物は遠ければ遠いほど大きくみえる。
短い距離では遠いものほど小さく見えるという幾何学が成立するが、光が伝わる間に宇宙が何倍にも膨張するほどの距離ではその限りではない。
もっとも、初期宇宙の幼い銀河はまだ暗くて小さい傾向にある。天体自体が小さいことは宇宙膨張による拡大効果を打ち消してしまうので、実物の写真を見てもでかいという印象は受けないだろう。これは近くにいる大人と遠くにいる(ので拡大されて見える)赤ん坊を比較するようなものだ。
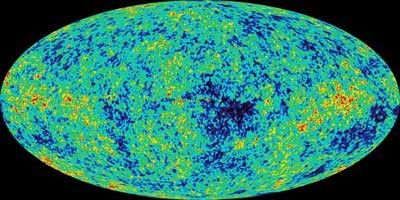
Fig6. でかく見える例:宇宙マイクロ波背景放射(CMB)
ビックバンから約38万年後に、不透明なプラズマだった宇宙は十分に冷えて透明な水素ガスになる。この境界(CMB)*5は光で観測できる宇宙の果てであり、どの方向をみてもマイクロ波で光る雲壁として観測される(上図はWMAP衛星で観測したCMBの全天パノラマ)。
- CMBには数十万光年サイズのむらむらが存在しているが、遠い宇宙の果てにあるので見かけは満月よりも大きい。
- むらと同サイズの天体を10億光年(LTD)しか離れていないところに置いたら、点にしか見えない。
- もしCMBの壁を越えてさらに遠くを観測できる手法が確立されたら、さらに小さかった時代の宇宙が際限なく拡大されて見えるだろう。
A5. 光度距離:宇宙の果てに近い天体は無限に暗い
超遠方宇宙からくる信号はとても微かだ。
宇宙がX倍に膨張すると、光のエネルギー密度はX^4倍に希釈される。Z=9 (X=10) にある天体の表面輝度は、宇宙膨張の効果で1/10000になってしまう。像の面積が100倍になるので、トータルの明るさは1/100どまりだが、像が広がった分ノイズが増えることも含めて厳しいことにかわりない。
銀河系近傍で物体の明るさは距離の2乗に反比例する。例えば光源までの距離が3倍になると、見かけの明るさは1/9だ。明るさを基準にした距離を光度距離(LD: luminosity distance)という。同じ光源を2つ用意して、明るさが1/100に見えるなら10倍の距離にあると考える。
超遠方天体の暗さたるや、宇宙で最初に生まれた星々までの距離は1兆光年(LD)に達し、CMBに至っては50兆光年(LD)にもなる。光度距離で1 兆光年とは1億光年離れた状況のさらに1億分の一の明るさになる距離ということ。
光度距離での圧倒的な宇宙の深さは、遠い宇宙を観測困難にする要因の一つだ。
B. 加速膨張について
B1. 自然な宇宙膨張は減速膨張
A2でみたように、観測される宇宙は一貫して膨張している。赤方偏移は過去に遡るほど大きく(Fig2)、現在と比較した宇宙の大きさ 1/(1+Z) は過去に遡るほど小さい。
では、宇宙膨張のペースは未来も過去も同じだろうか。
宇宙膨張は相対性理論に拡張された重力の振る舞いであり、普通の物質ならお互いに引き寄せ合あって膨張を減速させる方向に働く。
ニュートン的重力によるアナロジーだと、空に向かって投げたボールが重力で地球に引き戻される現象が近い。ボールが脱出速度を超えていて無限の彼方に飛び去るにせよ(永久膨張)、ふたたび地上に引き戻されるにせよ(ビッグクランチ)、重力はボールに対して引力として作用する。
ボールを投げてしばらくしたら、ぐんぐん天に向かって加速し無限に速くなっていく(加速膨張)という現象があるとしたら、重力の性質としていかにも不可解だ。
B2. 宇宙年齢のパラドックス、加速膨張の兆候
しかし減速膨張で計算すると、宇宙が中身である銀河や星より若いというパラドックスが生じうる。近傍銀河を使った現在の膨張速度の測定結果を用い、過去はさらに膨張が速かったのだとすると、宇宙は例えば90億歳だということになってしまう。
当時は宇宙年齢の測定精度が低いとは言え、ある球状星団などは200億歳ぐらいあるんじゃないかみたいなことも言われていて*6、「宇宙項(暗黒エネルギー)のような変なものを導入すれば、宇宙膨張の減速を緩和できる。宇宙年齢が伸びて問題は解決する。」といった議論がなされた。
Fig7. 宇宙膨張の時間変化
横軸は時間(単位は十億年)、縦軸(左)は現在と比較した宇宙の大きさである。
減速膨張(過去はもっと膨張が速い)だと宇宙年齢が短くなってしまうが、宇宙項などをいれて膨張速度を調整してやると宇宙年齢を伸ばすことができる。
B3. 実際に測ってみる:2011年ノーベル物理学賞
言うだけならどんな妄想も可能だ。加速膨張が科学たるためには実際に過去の膨張速度を測ってやる必要がある。
極めて遠方の天体を観測した場合、当時の宇宙の大きさは赤方偏移でわかる*7が、当時が宇宙年齢で何億歳に相当するか正確に測るのは難しい。
そこで宇宙年齢より正確に測れる天体の明るさ(光度距離)を使う。天体までの光度距離は、真の明るさが十分に理解されている天体があれば正確に測定できる。ちょうどいいところにIa型超新星*8という定格光度の照明弾がころがっているのでこれを使うことにしよう。
宇宙が加速膨張していると、ある赤方偏移Zに対して光度距離が大きく(天体が暗く)でる傾向にある。それを実際に測ったのが次の結果
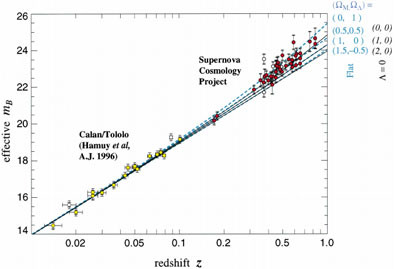
Fig8. Ia型超新星の明るさと赤方偏移の関係
横軸は赤方偏移、縦軸は超新星の明るさ(数値が大きいほど暗い):
Zが大きいところで観測値が系統的に暗くシフトしていることは、宇宙の加速膨張を示唆する。簡単な観測のように思われるかも知れないが、感度と視野角で現代に遠く及ばない90年代は、Z~1に達するような遠方の超新星を多数測定することは大変だったようだ。Measurements of Ω and Λ from 42 High-Redshift Supernovae - IOPscience
これだけだと遠方超新星を暗くする別の説明がいくらでも考えられそうだが、その後より多くの超新星について研究され、また銀河団や宇宙背景放射の精密測定などにより*9、加速膨張とそれを起こしうる物理的起源(「暗黒エネルギー」のようなもの)が受け入れられるようになってきた。
C. 以下、脈絡の無い雑記
冒頭で誤解として挙げておきながら触れなかったことなど
- 曲率の説明を省いているけど、あるとすれば次回。適当に3角形を作った場合、内角の和が180°より大きくなるか、小さくなるか、それともユークリッド空間のように180°ピッタリになるかというパラメタがある。遠くの宇宙の見え方がちょっと異なる。
- 原子や太陽系は宇宙膨張で膨らまない*10。銀河団も自己重力の影響が卓越していてわりと切り離されている。超銀河団やさらに大きい構造になると団結心に欠けるのでそこそこ影響を受ける。
- LTDみたいな腐った物差と比較してばかりで、本来の幾何学的な距離である固有距離や共動距離に触れないことに対してツッコミがあるかもしれない。申し訳程度に対応関係に触れておくと、観測可能な宇宙の果てまでの共動距離は約470億光年、Z=10で約250億光年、Z=1で約100億光年といったところ。宇宙の大部分はhigh-Z
- 固有距離が超光速で離れている領域からの光や情報は地球に届きうる(地平線はもうすこし遠い)。大域的な後退速度が光速を越える距離にあまり物理的な意味はない。
- 宇宙膨張下で離れたところに情報が伝わる速度などの量的な関係は話題が発散するので今回は略
- 星と星は凄まじく孤立しているけど、銀河と銀河の距離はそうでもない。例えば局部銀河群だと10万光年ぐらいの銀河が200万光年しか離れていない。星と違い銀河同士はよく交通事故を起こしている。
*1:輻射優勢期:輻射がエネルギー密度の主要部を占め、宇宙膨張の主役だった時代。ビックバンから数万年後、宇宙の晴れ上がりの少し前に終了する。
*2:CMBを除く
*3:私たちが特別な宇宙の中心にいることを意味しているのはなく、宇宙のどこにいても137億光年(LTD)先がビッグバンになってみえる。また、私たちから見て同じ方向に129億光年(LTD)離れた天体Aと135億光年(LTD)離れた天体Bがあった場合、AからみてBが6億光年(LTD)より遥かに大きく離れていることに注意しよう。宇宙論的距離で単純な足し算・引き算にならない。
*5:Z~1100、LTD~137億光年
*6:今は、星風をちゃんと考慮することで200億歳もないと考えられるようになった。
*7:当時の宇宙の大きさは1/(1+Z)倍
*8:Ia型超新星は、白色矮星がガスを食べたりして一定の質量に達したときに暴走的な核反応が生じて木っ端微塵になる現象で、明るさが精度良く理解されている。核燃料が同じで、太陽の約1.4倍という決まった質量をもった天然の原子爆弾だ。
*9:銀河団の観測から暗黒物質を含めた”物質”の総量を測定することができるが、物質だけではWMAP等の観測による平坦な宇宙を実現するに足りない
*10:微細構造定数がZ依存するかも、みたいな話はあるが