阪大入試をダシに音波の話
阪大の物理の入試問題の誤りが局所的に話題になっている。
平成29年度大阪大学一般入試(前期日程)等の理科(物理)における出題及び採点の誤りについて — 大阪大学
このたび、本学において、平成29年度大阪大学一般入試(前期日程)等の理科(物理)における出題及び採点に誤りがあったことが判明いたしました。そのため、改めて採点及び合格者判定を行い、新たに30名を合格者としました。
問題の正答について話が錯綜する中で,音波という現象の振る舞いに一部で混乱もみられるので,すこし考えを整理しておこう。
音波の反射に関する位相の扱いが難しいという感想も出ているが,QCDなどに比べれば単純な数学であり,単に慣れていないだけだろうと考えている。
まずは関係式
粗密がどうだとか変位がどうのだとか自然言語でごちゃごちゃ書いたところで混乱が深まるばかりなので,はじめに音波(微小摂動の弾性による伝搬)における各物理量の関係を書いておく。媒質の変位の分布をXとするとき,流速,密度,圧力の微小摂動は次の関係で表される。
\begin{align}
& \delta u = \frac{\partial X(t,x)}{\partial t} \tag{1} \\
& \delta \rho = -\rho_0 \frac{\partial X(t,x)}{\partial x} \tag{2}\\
& \delta p = c^2 \delta \rho = -\rho_0 c^2 \frac{\partial X(t,x)}{\partial x} \tag{3}
\end{align}
媒質の運動速度は変位Xの時間変化率であり,圧力変化
は変位Xの空間勾配(体積の変化率に比例)に比例する。(1)-(3)は運動方程式(オイラー方程式)や状態方程式から導出されるもので,壁の中だろうが空気中だろうが水中だろうが成立する。
反射という現象
反射という現象は,密度や音速が不連続になっているところで発生する。密度や音速が異なれば同じ組成(例えば冷水と温水の接触面)でも構わない。
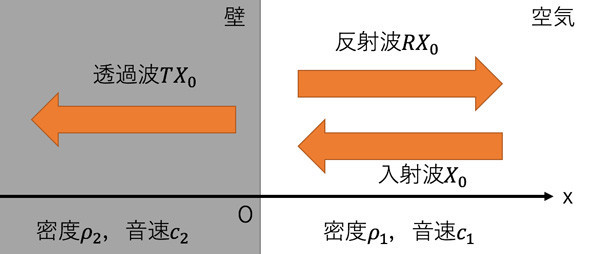
図のような反射を考え,不連続面を挟んで以下の境界条件を課す。
- 圧力は連続である。(衝撃波のような極端な圧力波を考えない)
- 変位は連続的である。(例えば,空気と壁の間に隙間(真空)ができたり,空気が壁に染み込んだりしない)
変位でみた反射波・透過波の複素振幅を適当な係数R, T を使って(4)のようにおく。この時点では,反射波の位相について何も仮定されていない。
\begin{align}
& X = X_0 e^{i\omega (t - x/c_1)} + RX_0 e^{i\omega (t + x/c_1)} = TX_0 e^{i\omega (t - x/c_2)} \tag{4}\\
\end{align}
あとは圧力が連続であるという要請と,最初に示した式から流速や圧力の摂動がすぐに決まる。
\begin{align}
& \delta u = i\omega X_0 e^{i\omega (t - x/c_1)} + i\omega RX_0 e^{i\omega (t + x/c_1)} = i\omega TX_0 e^{i\omega (t - x/c_2)} \tag{5}\\ \label{aaa}
& \delta p = i\omega \rho_1 c_1 X_0 e^{i\omega (t - x/c_1)} - i\omega \rho_1 c_1 RX_0 e^{i\omega (t + x/c_1)} = i\omega \rho_2 c_2 TX_0 e^{i\omega (t - x/c_2)} \tag{6}
\end{align}
反射波や透過波に関する,欲しい各物理量の振幅・位相の関係は,(4)-(6)で概ね語り尽くされている。
反射波,透過波の複素振幅を決める係数R,Tは,(5)-(6)を連立することで得る。
\begin{align}
& R=\frac{\rho_1c_1 - \rho_2 c_2}{\rho_1c_1 + \rho_2 c_2} & T=\frac{ 2 \rho_1c_1}{\rho_1c_1 + \rho_2 c_2} \tag{7}
\end{align}
最初に着目する物理量はどれでもいい
音波の伝搬においては変位,流速,圧力,温度,すべてが変化する。これらは単純な関係(微分とか)でつながっていて,ぜんぶ整合的に動く。変位に着目しようが圧力偏差に着目しようが,粗密に着目しようが音波という現象はひとつである。
特定の物理量XXXの摂動が本質という事はない。
反射波の変位の同位相・逆位相は密度ρと音速cの積ρcが決める
(7)では圧力ρと音速cの積ρcが反射波の複素振幅を決めている。ρcを音響インピーダンスといい,基本的*1に壁のインピーダンスは空気のインピーダンス
より大きいので,Rは負であり,反射波の変位は逆位相。
\begin{align}
& R=\frac{\rho_1c_1 - \rho_2 c_2}{\rho_1c_1 + \rho_2 c_2} = \frac{Z_1- Z_2}{Z_1 + Z_2} < 0 \tag{8}
\end{align}
位相変化量は物理量によって異なる
Rが負であることを踏まえて,(5)-(6)をみると,空気中を伝わってきた音波が硬い壁にぶつかる場合,圧力は同位相,変位や流速は逆位相で反射することが分かる。同位相・逆位相は着目する物理量によって異なるが,音波の反射というひとつの現象を,異なる視点から眺めたものに過ぎない。
入射側の音響インピーダンスの方が大きい場合
例えば,壁の中を伝わってきた音波が壁と空気の境界で反射する場合,Rは正であり,(4)-(6)から,圧力も変位も流速も同位相で反射する。
変位に関して縦波だから横波だからという議論はそこまで気にしなくていい
変位の向きこそ異なるが,横波である弦の振動だろうが,縦波である音波だろうが,変位や流速は境界(壁面とか端点とか)でほぼ0になる*2。
壁の反射は特に迷う所は無いが,音叉はすこし厄介だと考えている。
音源から放射される摂動の方位分布は,発生機構によって異なる。例えば爆弾の爆発なら東宝的に圧力波が広がるし,スピーカーのような膜振動なら双極的な放射になる。
現実の音叉から放射される音波は圧力に関して双極放射的なモードや四重極放射的なモード(こっちが卓越?)が混じっているようである。高調波を無視しても,Uが開いたり閉じたりする振動モード,捻るような振動モード,Uがまるとご揺れる振動モード(双極的な音圧を放射する)があり,箱との響鳴もそれなりに厄介そう。
それらを脇において,圧力摂動が四重極卓越であることを図1および問1が主張しているのであれば,(逆方向に向かう音波を比較した場合)圧力摂動に関して同位相,変位に関して逆位相の摂動を,放射していると見做せる。
一端そう読み取れば,音叉が居座るただ一点を覗いて,不穏な点はない。
音叉の特異点
音叉から放射される摂動の位相は,あくまでも,音叉から離れたところを記述しているものである。遠方の性質を,安直に音叉の位置まで繋いではいけない。
慎重な受験生は,問題文に書かれたように音叉を真に点音源だと見做してしまうと,音叉がまさに存在している位置の各物理量が不定か発散していることに気づくだろう。密度が連続で,流速が不連続な点は流体力学の基本法則が許さない。
どうしても発散を除きたい場合は,無限小ではなく有限サイズを仮定して音叉近傍の複雑な場を計算するか,潮汐変形する(有限サイズの)より単純な物体(ただし壁からの反射波は横を素通りするものとする)あたりで代用することになると考えている
最後に
限られた解答時間でどこまでの現象認識と割り切り判断が受験生に求められていたか微妙だが,当事者でない身には音波という現象をいろいろな人が再確認するよい機会
